Úloha: Máte úsečky délek a, b a c. Sestrojte úsečku délky \(\sqrt{abc}\). nemůže mít řešení, protože \(\sqrt{cm^3}\) není cm, tudíž to není délka.
Nic proti tomu argumentu, ale co kdybychom to zadání formulovali trochu jinak:
Máte úsečky délek a cm, b cm a c cm . Sestrojte úsečku délky \(\sqrt{abc}\) cm.
Teď provádíme jen číselné operace. Má tato úloha řešení? Podobné důkazy se nejsnáze provádějí tak, že se to řešení najde.
Sestrojit úsečku délky \(\sqrt{ab}\) by nebyl problém. Stačí si vzpomenout na Euklidovu větu o výšce. Konstrukce je vidět i na přiloženém obrázku. Jenže v zadání jsou činitelé tři.
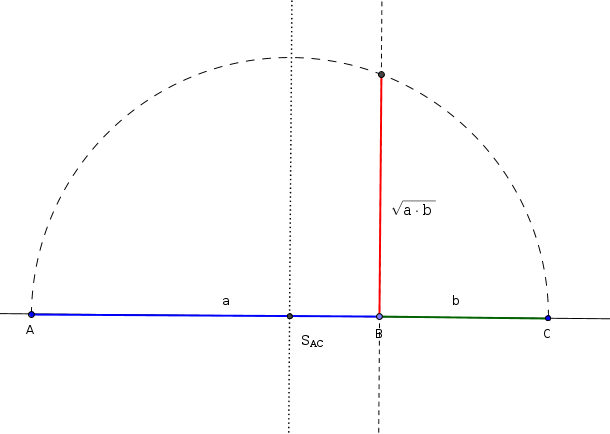
Tenhle problém se mi nedávno v jakési volné chvíli vybavil a ukrátil mi cestu vlakem. Po několika zastávkách jsem tušil, co potřebuji dát dohromady.
- \( \sqrt{abc} = \sqrt{ab} \cdot \sqrt c \)
- umím sestrojit \(\sqrt{ab} = d\)
- sestrojím součin \(ab = d^2\)
- sestrojím \(\sqrt{dc}\)
- mám řešení
Je jasné, že pes je zakopaný ve třetím kroku. Přemýšlel jsem, jak geometricky získat úsečku, jejíž délka je číselně rovna druhé mocnině číselné délky zadané úsečky. A pak mě napadlo použít euklidovu větu o výšce obráceně.
Euklidova věta pro výšku v pravoúhlého trojúhelníka ABC, která dělí jeho přeponu na díly ca a cb říká, že \( c_a \cdot c_b = v^2\). Pokud rovnici odmocníme (a na znaménka se nemusíme ohlížet, uvažujeme o délkách úseček), dostaneme:
\[ \sqrt{c_a \cdot c_b} = \sqrt{v^2}. \]
Pokud bude cb jednotková úsečka, pak musí platit identita \( c_b = v^2\). A k tomu jsme se chtěli dostat.
Takže jak na to? Máme výšku, na ní sestrojíme kolmici, na které určitě leží základna trojúhelníka, pro který jsme Euklidovu větu použili. Na tuto základnu naneseme jednotkovou úsečku cb. A teď už jen najít kde leží konec ca. Poslední fígl spočívá v tom, že trojúhelník, pro který Euklidova věta platí, je pravoúhlý. Jeho vrchol tedy leží na kružnici a my potřebujeme najít její střed. Námi hledaný poslední bod leží na této kružnici.
- máme úsečku AB délky a
- v jednom jejím koncovém bodě B k ní sestrojíme kolmici p
- na tuto kolmici z bodu B naneseme úsečku jednotkové délky, získáme bod C
- hledáme střed kružnice k, na níž leží body B a C a její střed leží na kolmici p
- sestrojíme osu o úsečky AC. Střed S kružnice k leží v průsečíku p a o.
- sestrojíme kružnici k se středem S a poloměrem SC. Najdeme bod D v průsečíku k a p
- úsečka BD má délku a2
Trochu jednodušeji tuto konstrukci ukazuje obrázek.

A teď už to stačí jen dát dohromady a úsečka délky \(\sqrt{abc}\) je na světě.